DEWI RATNA SARI, S. Pd: MATEMATIKA : VOLUME BANGUN RUANG GABUNGAN

Assallamuallaikum Wr Wb
selamat Pagi anak-anak hari ini kita akan belajar Matematika tentang Volume bangun Ruang gabungan

Siapkan Buku tulis matematikamu, sebelum itu jangan berdoa ya

Volume Gabungan Kubus dan Balok

PERHATIKAN VIDIO BERIKUT

VIDIO 1

VIDIO 2

VIDIO 3

Pertama adalah gabungan dua bangun ruang berbentuk kubus dan balok. Cara menghitung volume gabungan bangun tersebut adalah menjumlahkan masing – masing volumenya. Besar volume kubus dapat diperoleh melalui panjang sisi pangkat tiga. Sedangkan volume balok diperoleh dengan mengalikan nilai panjang, lebar, dan tinggi.

Misalkan, terdapat sebuah kubus dan balok bergabung menjadi satu sehingga terbentuk sebuah bangun ruang bentuk baru. Posisi kubus berada di atas balok dengan ukuran sisi kubus sama dengan lebar balok. Besar panjang, lebar, dan tinggi balok serta sisi kubus diberikan seperti gambar di bawah.

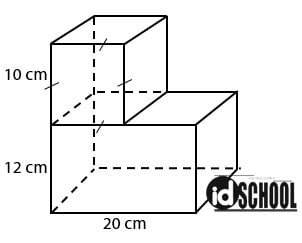
Selanjutnya, akan dicari besar volume gabungan dari bangun di atas.

Dikethaui:

sisi kubus = lebar balok: s = ℓ = 10 cm
panjang balok: p = 20 cm
tinggi balok: t = 12 cm

Menghitung volume kubus:

Vkubus = s3
= 103
= 10 × 10 × 10
= 1.000 cm3

Menghitung volume balok:

Vbalok = p × ℓ × t
= 20 × 10 × 12
= 2.400 cm3

Jadi besar volume gabungan kubus dan balok tesebut adalah
= Vkubus + Vbalok
= 1.000 + 2.400
= 3.400 cm3

Volume Gabungan Kubus dan Prisma

Berikutnya adalah volume bangun yang terbentuk dari kubus dan prisma segitiga. Volume bangun tersebut dapat dihitung dengan menjumlahkan volume kubus dan volume prisma. Oleh karenanya, sobat idschool perlu tahu bagaimana rumus untuk menghitung masing volume kubus dan prisma. Kedua rumus tersebut diberikan seperti pada bagian awal. Sebagai contoh, perhatikan soal beserta pembahasannya berikut.

Perhatikan gambar di bawah!

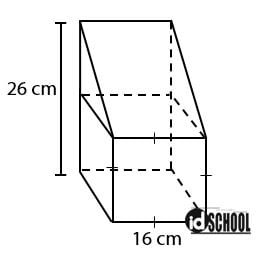
Volume bangun tersebut adalah ….
A. 6.776 cm3
B. 5.376 cm3
C. 4.408 cm3
D. 4.098 cm3

Pembahasan:

Diketahui:

sisi kubus: s = 16 cm
tinggi prisma: t = 16 cm
alas prisma berbentuk segitiga:
*alas segitiga (a∆) = sisi kubus = 16
*tinggi segitiga (t∆) = 26 – 16 = 10 cm

Menghitung volume kubus:

Vkubus = s3
Vkubus = s × s × s
Vkubus = 16 × 16 × 16
Vkubus = 4.096 cm3

Menghitung volume prisma:

Vprisma = Lalas × tprisma
Vprisma = (½ × a∆ × t∆) × 16
Vprisma = (½ × 16 × 10) × 16
Vprisma = 1.280 cm3

Jadi, volume tersebut adalah 4.096 + 1.280 = 5.376 cm3.

Jawaban: B

Volume Gabungan Balok dan Limas

Bentuk bangun ketiga merupakan volume gabungan dari bangun ruang berbentuk balok dan limas. Sama seperti kedua bentuk bangun ruang sebelumnya. Untuk mendapatkan volume gabungan ini perlu menghitung besar volume masing – masing bangun satu per satu. Contoh soal beserta cara menghitungnya dapat disimak pada soal berikut.

Perhatikan gambar berikut!

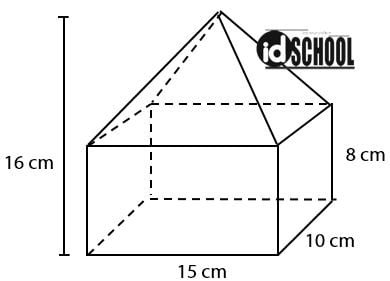
Volume bangun tersebut adalah ….
A. 1.600 cm3
B. 1.800 cm3
C. 2.100 cm3
D. 3.000 cm3

Pembahasan:

Bangun pada soal terdiri dari gabungan bangun limas dan balok.

Diketahui:

Panjang balok: p = 15 cm
Lebar balok: ℓ = 10 cm
Tinggi balok: t = 8 cm
Tinggi limas: 16 – 8 = 8 cm
Alas limas berbentuk persegi panjang:
*panjang persegi panjang (pp): 15
*lebar persegi panjang (ℓp): 10 cm

Menghitung volume balok:

Vbalok = p × ℓ × t
Vbalok = 15 × 10 × 8
Vbalok = 1.200 cm3

Menghitung volume limas:

Vlimas = ⅓ × Lalas × tlimas
Vlimas = ⅓ × (15 × 10) × 8
Vlimas = ⅓ × 150 × 8
Vlimas = 50 × 8
Vlimas = 400 cm3

Jadi, volume bangun tersebut adalah 1.200 + 400 = 1.600 cm3.

Jawaban: A

Volume Gabungan Balok dan Tabung

Keempat merupakan volume yang terbentuk dari bangun berbentuk balok dan setengah tabung. Volume balok dapat dihitung menggunakan rumus Vbalok = p × ℓ × t. Volume setengah tabung dapat diperoleh melalui volume tabung dengan ukuran yang sama dibagi dua, V½tabung = ½ × π × r2 × ttabung. Untuk lebih jelasnya simak contoh soal beserta pembahasannya berikut.

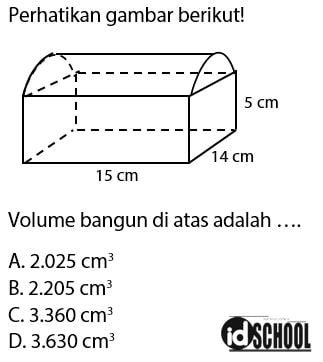
Pembahasan:

Bangun yang diberikan terdiri dari bangun ruang berbentuk balok dan setengah tabung.

Diketahui:

Panjang balok: p = 15 cm
Lebar balok: ℓ = 14 cm
Tinggi balok: t = 5 cm
Jari – jari tabung = ½ lebar balok: r = ½ × 14 = 7 cm
Tinggi tabung = panjang balok: ttabung = 15 cm

Menghitung volume balok:

Vbalok = p × ℓ × t
Vbalok = 15 × 14 × 5
Vbalok = 1.050 cm3

Menghitung volume ½ tabung:

V½tabung = ½ × π × r2 × ttabung
V½tabung = ½ × 22/7 × 72 × 15
V½tabung = ½ × 22/7 × 49× 15
V½tabung = 1.155 cm3

Jadi, volume gabungan bangun sama dengan 1.050 + 1.155 = 2.205 cm3.

Jawaban: B

Volume Gabungan Bola dan Tabung

Bangun kelima yang diberikan di sini merupakan bangun ruang yang terdiri dari setengah bola dan tabung. Cara menghitung volume tabung dapat diperoleh menggunakan rumus V½tabung = ½ × π × r2 × ttabung. Sedangkan besar volume setengah bola sama dengan volume bola (dengan ukuran sama) dibagi dua. Untuk menambah pemahaman sobat idschool, simak contoh soal dan pembahasan menghitung volume gabungan berikut.

Perhatikan gambar di bawah!

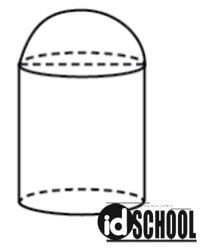
Diketahui panjang jari – jari alas 7 cm dan tinggi tabung 10 cm. Volume benda tersebut adalah …. ( π = 22/7)
A.     2.258,67 cm3
B.     2.618,33 cm3
C.     2.926,67 cm3
D.     2.977,33 cm3

Pembahasan:

Bangun yang diberikan pada soal merupakan gabungan dua bangun yang terdiri dari tabung dan setengah bola.

Mencari volume tabung:

Vtabung = πr2t
Vtabung = 22/7 × 72 ×10
Vtabung = 1.540 cm3

Mencari volume setengah bola:
V½bola = ½ × Vbola
V½bola = ½ × 4/3 × π × r3
V½bola = ½ × 4/3 × 22/7 × 73
V½bola = ½ × 4.312/3
V½bola = 4.312/6
V½bola = 718,67 cm3